Знали в школе, но забыли: как вычислить площадь треугольника и зачем это нужно

Что такое треугольник и каким он бывает

Треугольник — это одна из самых простых и в то же время хитрых фигур в геометрии. У него всего три стороны и три вершины.

Треугольники делятся на несколько видов.

• В зависимости от размера углов они бывают остроугольные (все углы меньше 90°), тупоугольные (один угол больше 90°) и прямоугольные (угол строго 90°). Последний — «любимец» школьных задач.

• В зависимости от размера сторон выделяют равносторонние треугольники (все стороны одинаковые), равнобедренные (две стороны равны) и разносторонние (все стороны разные).

Для каждого вида треугольников применяются свои формулы площади.

Универсальные формулы площади треугольника

Вычислить площадь треугольника можно десятком способов, и в этом его прелесть, рассказала «Газете.Ru» учитель математики школы №64 города Самары, блогер Екатерина Комлева. В зависимости от того, какие данные у нас есть — стороны, углы или высота, — выбирайте нужную формулу.

1. Через основание и высоту

Классический вариант, знакомый каждому школьнику.

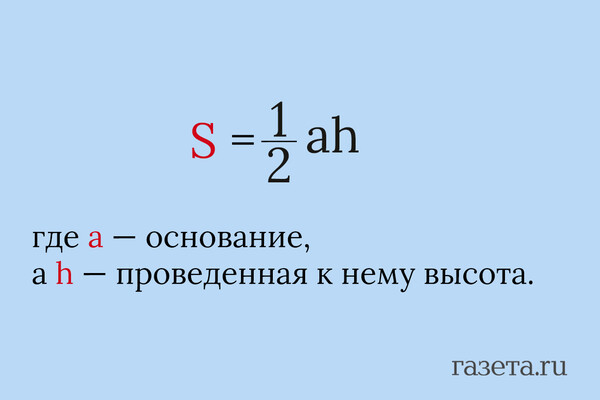
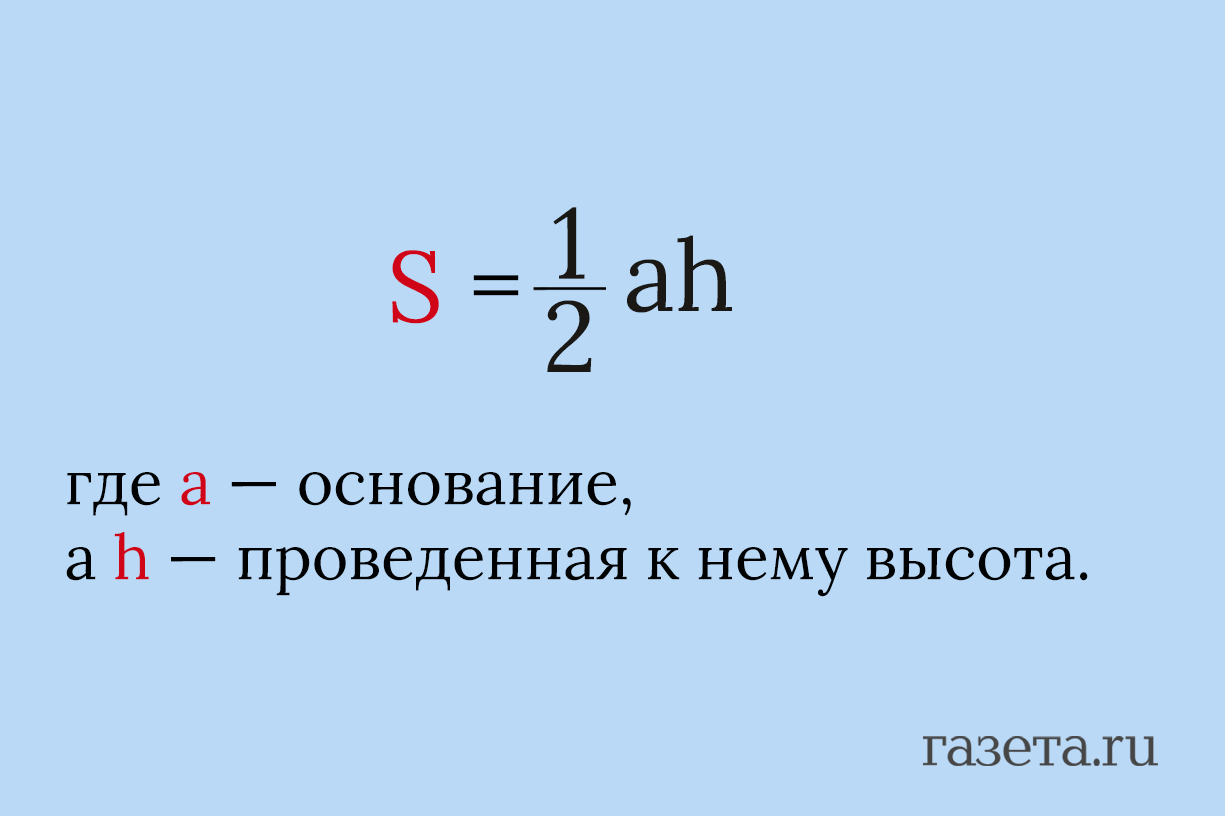
Формула работает для любого треугольника, нужно лишь знать хотя бы одну сторону и высоту, опущенную на нее.

2. Формула Герона

Когда высоту найти сложно, а стороны известны — выручает древнегреческий математик Герон со своей формулой.

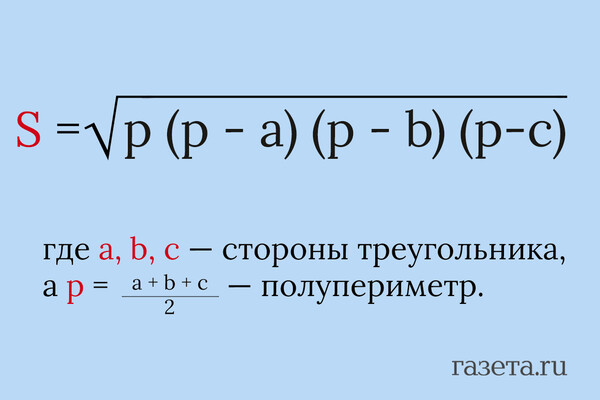
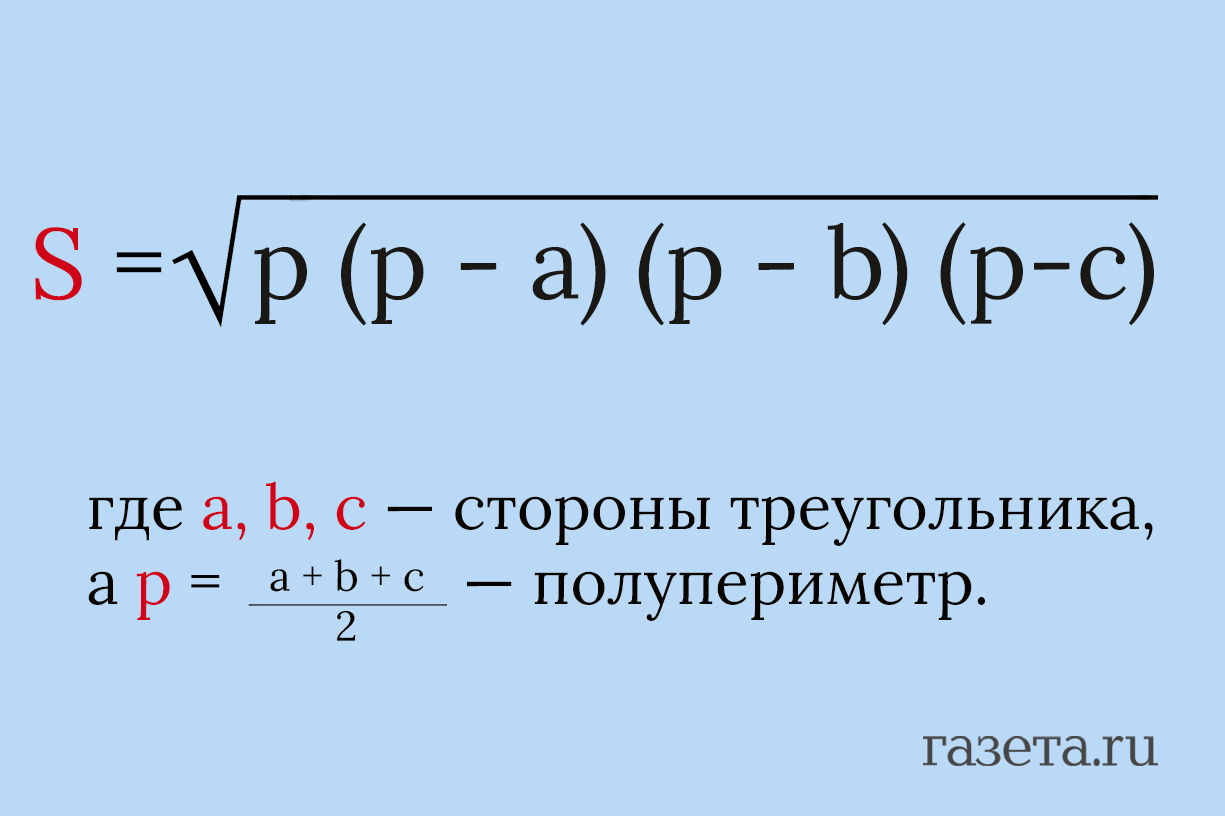
Эта формула хороша тем, что универсальна: подходит для любого треугольника, если известны три стороны, объяснила «Газете.Ru» ведущий методист по математике в онлайн-школе «Фоксфорд» Дарья Селукова. Используйте формулу Герона, когда известны все три стороны треугольника (a, b, c), но у вас нет информации об углах.

3. Через две стороны и угол

Если известны две стороны и угол между ними, площадь находится по формуле:

4. Через радиус вписанной в треугольник окружности

Такая формула применяется нечасто, но иногда она становится палочкой-выручалочкой.

Формулы площади прямоугольного треугольника

Прямоугольный треугольник — это тот самый случай, когда жизнь становится проще. Один угол в нем всегда равен 90°, и это открывает массу удобных способов вычисления площади.

Нужно запомнить некоторые сопутствующие термины. Сторона, противоположная прямому углу, называется гипотенузой. Стороны, прилегающие к прямому углу, — это катеты. Если катеты равны, то фигура называется равнобедренным прямоугольным треугольником.

1. Через катеты

Самая простая и популярная формула.

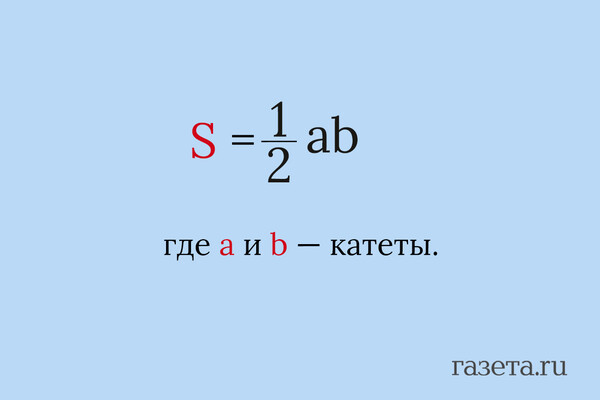
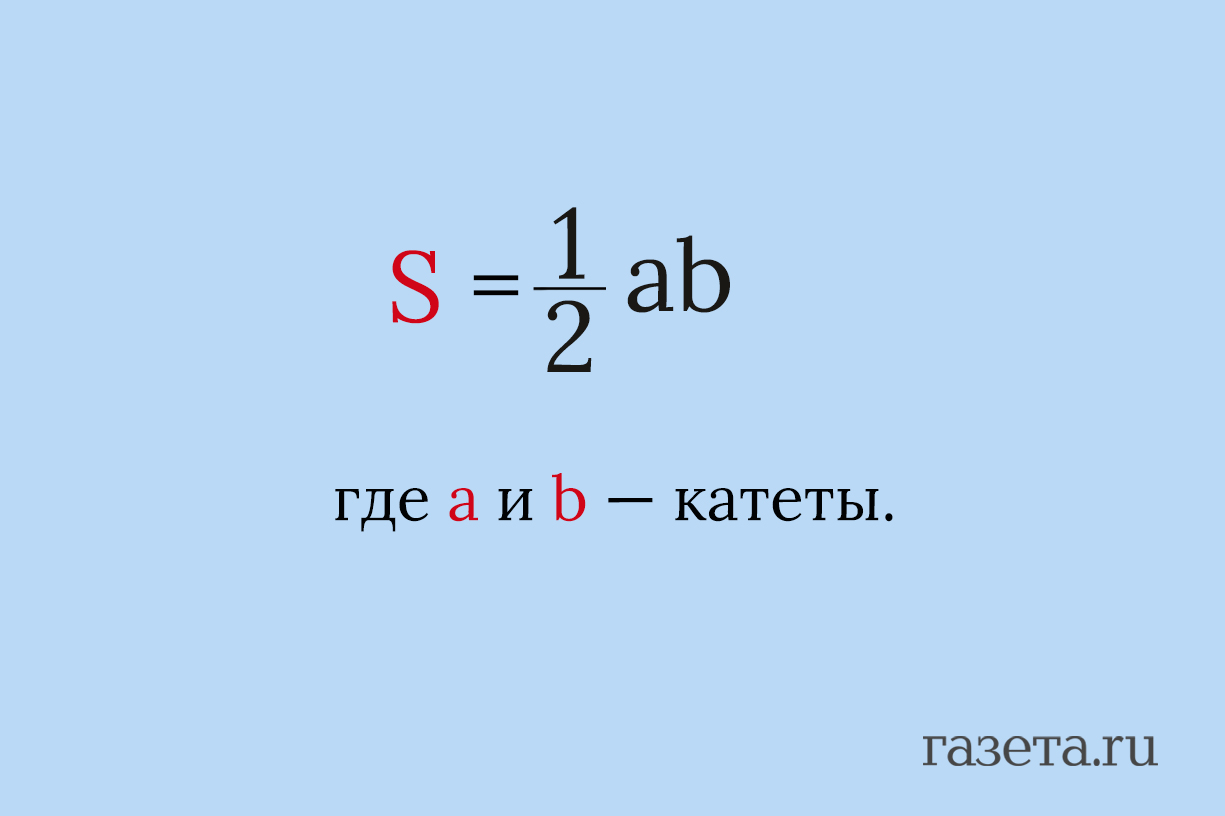
2. Через гипотенузу и высоту

Если известна гипотенуза c и высота h, проведенная к ней, площадь вычисляется так:

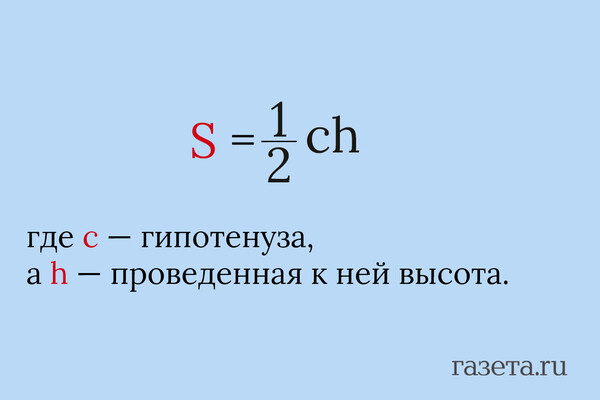
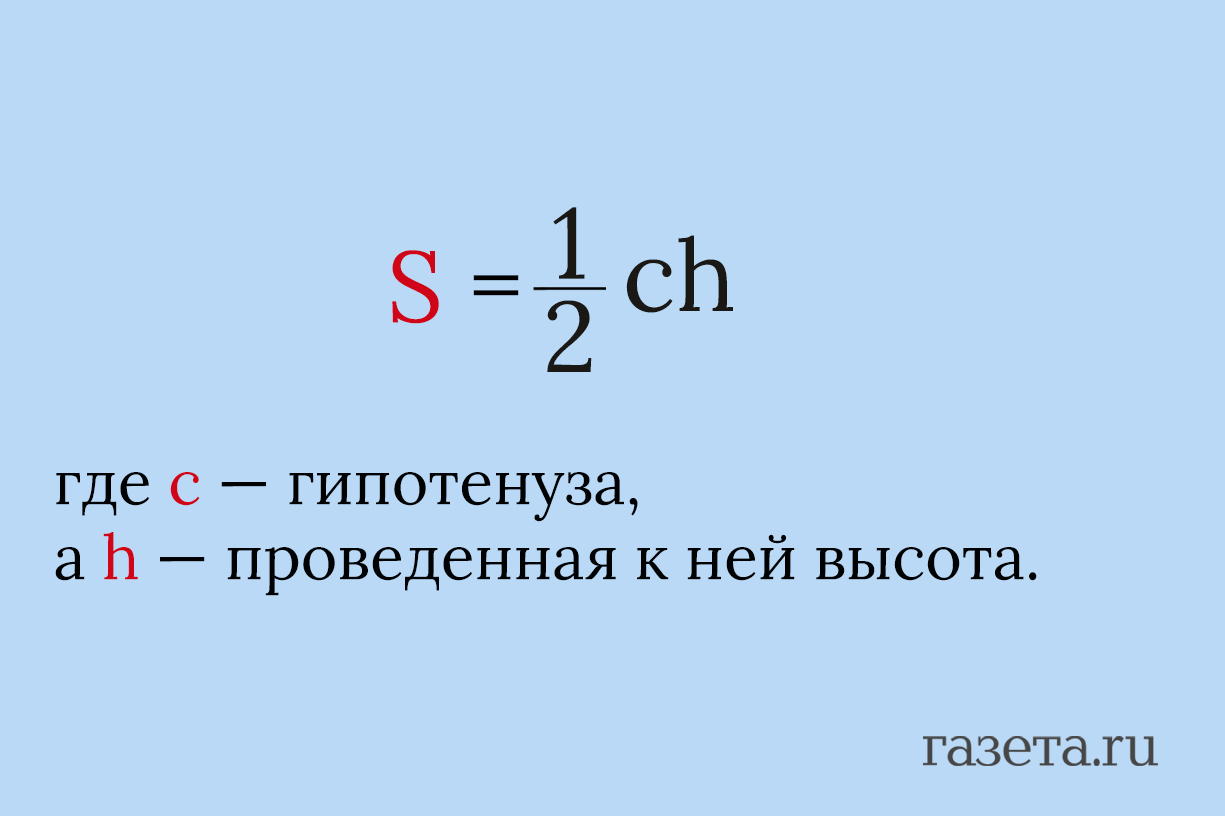
3. Через тангенс и котангенс

Когда даны катет и угол, можно использовать тригонометрию. В данных формулах а — катет, а α — прилежащий к нему острый угол, b — катет, а β — противолежащий к нему острый угол.

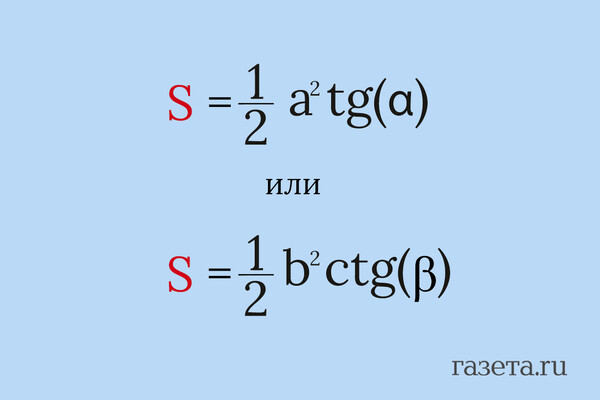
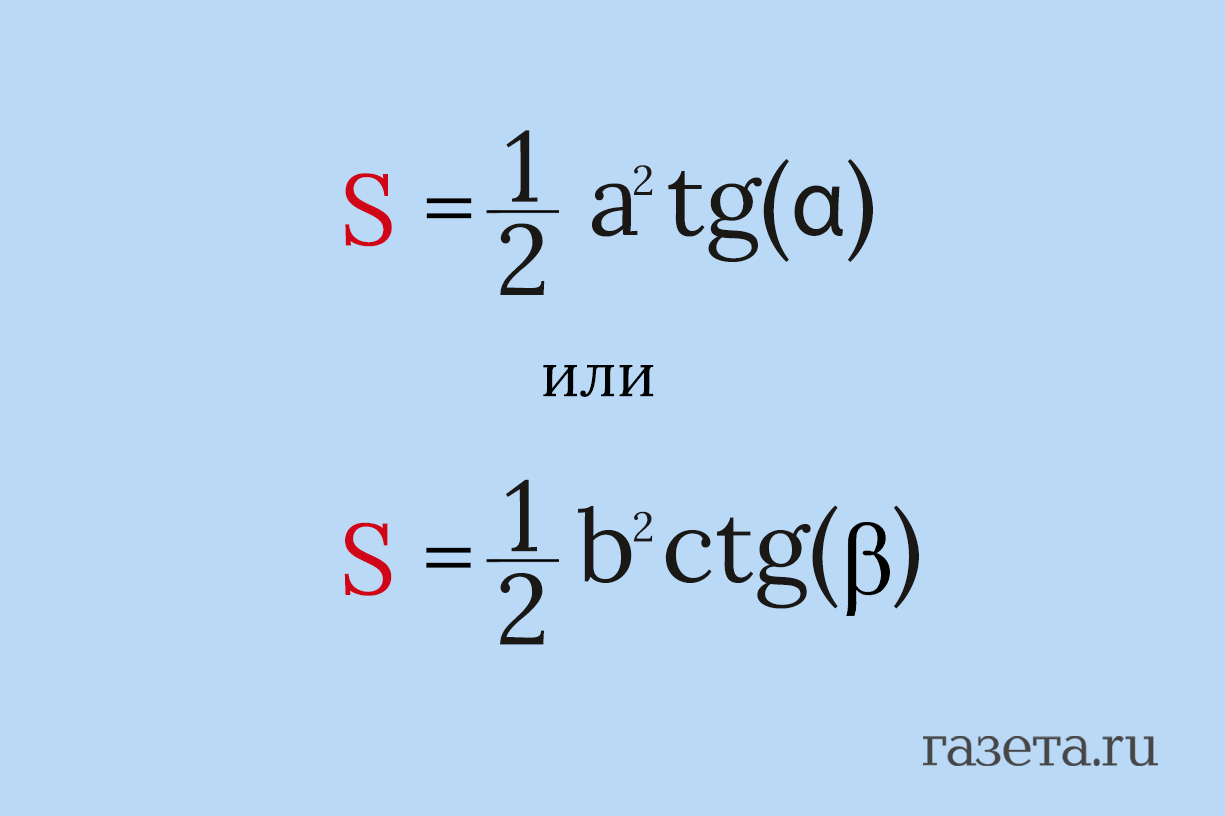
По словам Дарьи Селуковой, тригонометрические методы лучше использовать, когда известны две стороны и угол между ними. Она подчеркнула, что этот способ намного быстрее и удобнее формулы Герона, если известен угол. Вычисления обычно проще, особенно если углы «красивые»: 30°, 45°, 60°.

Формулы площади равнобедренного треугольника

У равнобедренного треугольника две стороны равны, а вместе с ними и углы при основании. Благодаря симметрии вычислить площадь становится проще.

1. Через основание и высоту

Классическая формула. Высота в равнобедренном треугольнике делит основание пополам и образует два прямоугольных треугольника.

2. Через боковую сторону и угол при вершине

3. Через основание и боковую сторону

Когда известны основание и боковая сторона, высоту можно вычислить по теореме Пифагора, а далее — площадь:

4. Через радиус вписанной или описанной окружности

Для равнобедренного треугольника такие варианты задач встречаются редко, но возможны:

В учебниках часто советуют начинать решение задач на площадь именно с равнобедренного треугольника: он наглядный и позволяет «увидеть» все взаимосвязи. С ним легче уловить, в чем смысл высоты, как считать площадь через углы и почему формулы разные, хотя результат один — цифра в квадратных единицах.

Формулы площади равностороннего треугольника

У равностороннего треугольника все стороны равны, как и все углы (каждый угол — 60°).

1. Через сторону

Самая известная формула.

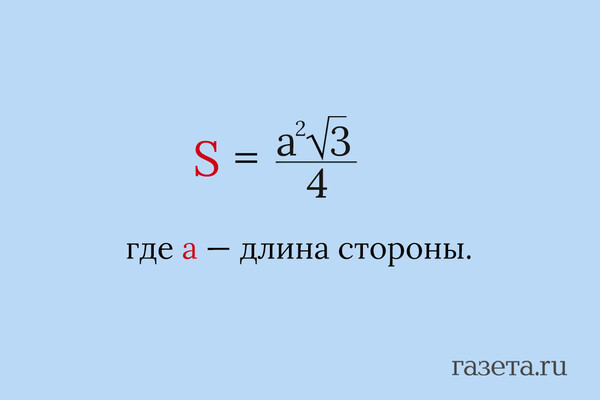
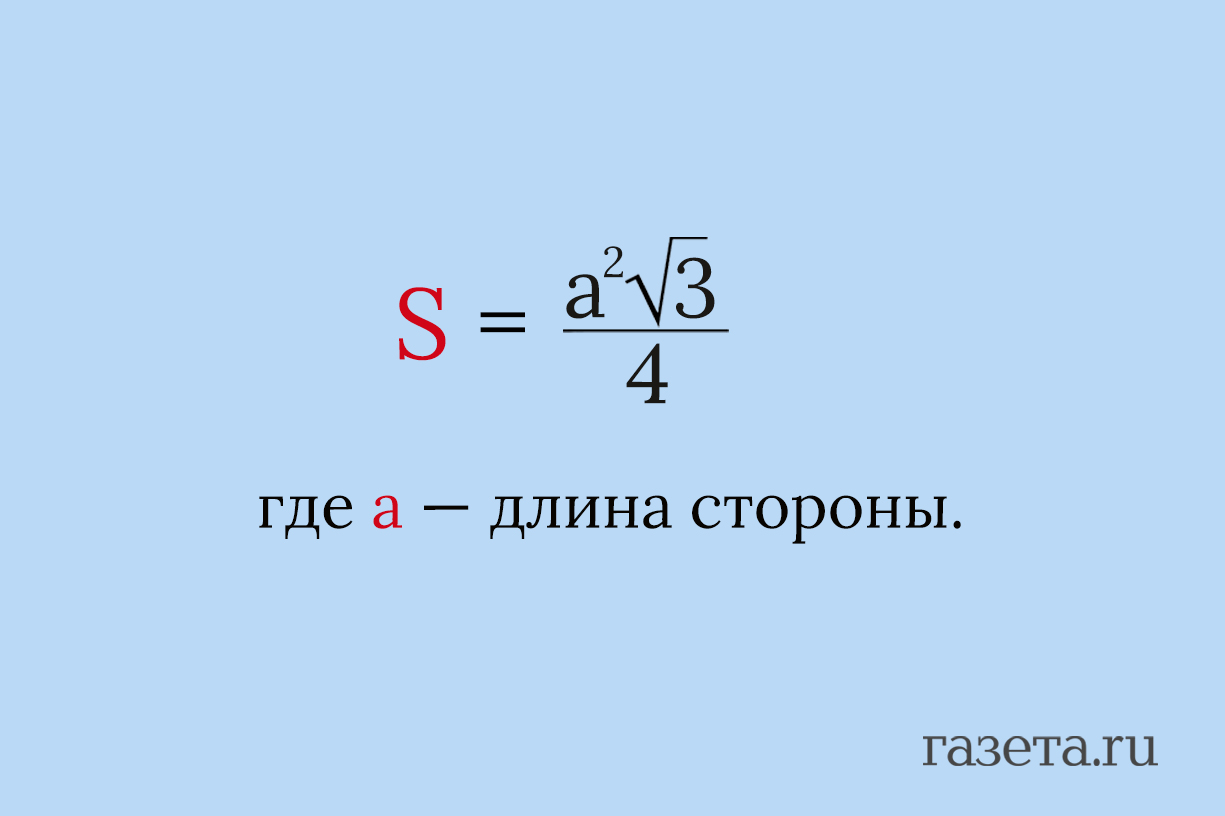
2. Через высоту

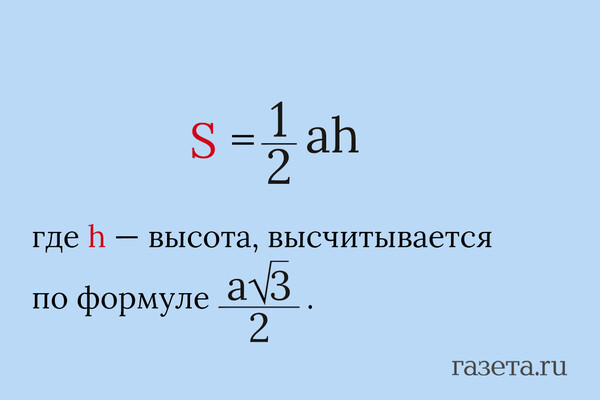
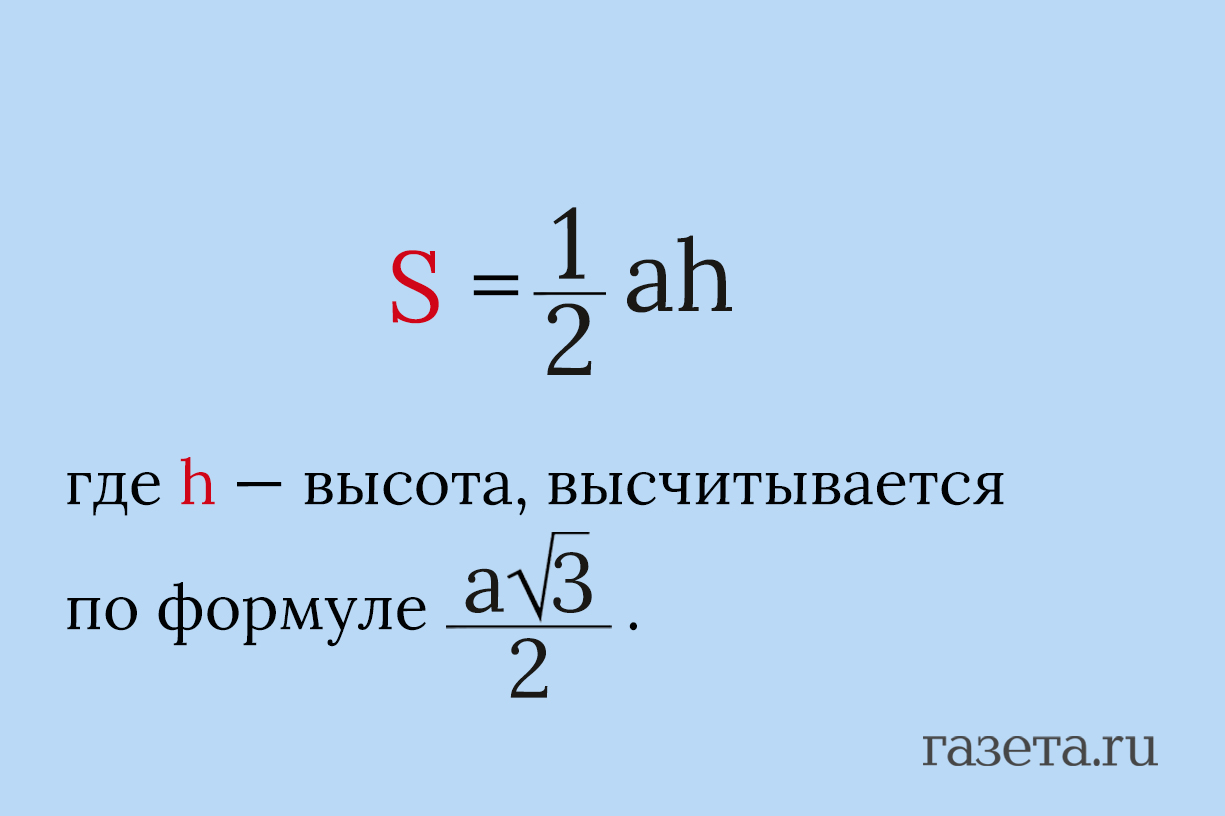
3. Через радиус вписанной окружности

4. Через радиус описанной окружности

Равносторонний треугольник удобен еще и тем, что его формулы часто применяются не только в задачах по геометрии, но и в физике, архитектуре, дизайне — везде, где нужна симметрия и расчет площади через одну единственную величину.

Где в реальной жизни пригодится площадь треугольника

Когда мы в школе зубрили формулы площади треугольника, многим казалось: «Ну и зачем мне это? Разве я собираюсь в жизни ежедневно строить пирамиды?» Но если посмотреть шире, треугольники окружают нас повсюду. А умение считать их площадь может пригодиться в самых неожиданных ситуациях, подчеркнула Екатерина Комлева.

Строительство и ремонт. Представьте, вы решаете обшить дом сайдингом или меняете кровлю. Фронтон крыши — это как раз треугольник. Зная его площадь, легко понять, сколько нужно материала, чтобы не купить лишнего и не бегать в магазин за недостающими листами. То же самое касается плитки, краски или любого отделочного покрытия.

Дизайн и архитектура. Треугольные формы любят архитекторы: витражи, декоративные панели, элементы ландшафта — все это требует точных расчетов площади. Ошибся на пару сантиметров — и готовая конструкция уже не встанет на место.

Геодезия и картография. При измерениях на местности большие фигуры часто разбивают на треугольники. Так проще посчитать площадь участка земли, леса или водоема. Карта в этом смысле — набор маленьких треугольников.

Швейное дело. Казалось бы, причем тут геометрия? Но попробуйте выкроить волан или косую бейку без расчета. Чтобы ткань не ушла впустую, портные тоже используют принципы геометрии, в том числе расчеты площади фигур.

Кулинария. Пицца, торты, пирожные — все эти «лакомые треугольники» иногда требуют точного знания размеров, чтобы рассчитать количество ингредиентов.

Методист по математике Дарья Селукова отмечает, что применение формул площади треугольника не ограничивается бытом. По ее словам, это порой помогает и в профессиональной сфере:

• определять площадь земельных участков неправильной формы, разбивая их на треугольники — это нужно, например, чтобы рассчитать количество семян для газона или объем удобрений для него;

• использовать метод триангуляции, который основан на свойствах треугольников, для определения положения объектов на местности и построения карт;

• рассчитывать прочность и устойчивость конструкций, где применяются треугольные элементы — например, в формах мостов или опорах башен, ведь треугольник считается самой жесткой геометрической фигурой.

В итоге знание формул площади треугольника оказывается не просто «школьным багажом», а практическим инструментом.

{
    "_essence": "video",
    "media_position": "bottom",
    "uid": "_id_video_media_22342537_rnd_5",
    "video_id": "record::09ff6336-5a9c-47fd-ab6f-f3697cfc5629"
}